This post is a little late than earlier ones. The semester has started and between all the classes and HWs, I get less time to focus on the projects I want to do. Other than that I had a lot of interviews for summer internship in the past month but no more interviews now :)
You probably are familiar with the problem with the internet- too much information and too little time. Machine learning drives the content you see everywhere on the internet, from friend suggestions on Facebook to where you might work on LinkedIn. Two philosophical approaches to do this are: recommend what is popular or try to understand the user’s taste. The personalized recommendations can either be derived using content-based or collaborative filtering methods (although modern recommendation systems combine both the approaches). Content-based methods use similarity between products as a measure and collaborative filtering tries to understand the interactions between users and items.
Collaborative filtering works on the principle of matrix factorization. Which matrix? Users as rows vs products as columns (or vice-versa) and ratings as values of the matrix. The ratings can either be binary (like vs hate) or discrete ({1,2,3,4,5}) or continuous ([1,5]). Typically, this matrix is highly sparse and the job of a data scientist is to construct a mapping that learns to predict a user’s interest based on the analysis of tastes and preference of other users in the system and implicitly inferring “similarity” between them. The assumption driving this is that people with similar tastes will also have the same opinion on an item than two people randomly chosen.
Coming back to matrix factorization, if X is your user-item matrix, then using Singular Value Decomposition, you can factorize your matrix as:
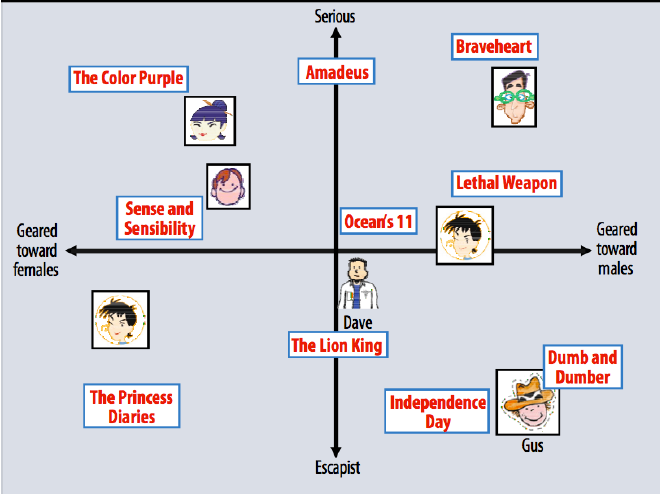
Each row of U represents the latent factors of each row of X, each column of V contains latent dimensions of columns of X and is a diagonal matrix holding the weight of each latent factor. Thus, A and B hold the k (chosen while hyperparameter tuning) latent dimensions connecting the users and movies. The final prediction for user i on product j is the inner product between a user’s preference for each latent factor and the product’s strength on that factor. An example of how some movies load on two latent variables:
In this project, I used Amazon Android Apps data to get ratings given by different users to different products. I sampled 240,000 users and their ratings on 14,000 apps (because that’s what my machine can handle). People have come up with many techniques to do the matrix factorization but the technique I found particularly interesting (and intuitive) was to use Autoencoders. Autoencoders have an encoding part which projects the n-dimensional input space to k-dimensional space and a decoding part which tries to reconstruct the n dimensions back from these k dimensions i.e. the objective function is to minimize the error between decode(encode(x)) and x, where x is the input instance of data. The k dimensional projection is similar to the k latent features you get from SVD and thus, autoencoder is an excellent tool for dimensionality reduction.
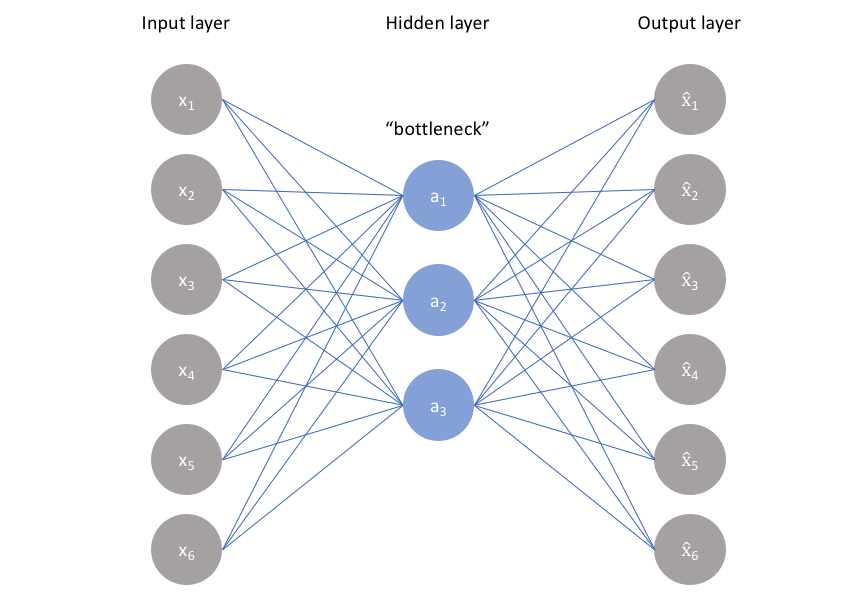
The input to this is the 14000 product reviews by any user and we want the autoencoder to replicate the input as output. Thus, for every missing value, I create a mask of zeroes for missing values and one if not missing. The mean square error between the input and masked output serves as the objective function which is minimized using Adam optimizer. I chose the evaluation metric to be RMSE (root mean square error) between predicted and actual ratings for users in the test set. RMSE tells us how much off our rating prediction is on average from the actual value. The autoencoder model I built consisted of 2 hidden layers in the encoder and 2 hidden layers in the decoder. The size of layers in the model was and all layers except the last one have ReLU as their activation function. After training for 40 epochs, the best model gave a holdout set RMSE of 0.942.

The next thing I tried out was dense refeeding, which is to take the unmasked output of the model and feed it back to the model as input. While refeeding, the new mask now has all ones because the output of autoencoder is dense. This step explicitly enforces fixed point constraint, i.e. for every input x, the model should learn f(x)=x. But I started dense refeeding after training the autoencoder without refeeding for 30 epochs and it takes a total of 60 epochs to train this network. This increase in learning time is expected because initially, it would be making more mistakes which it learns while refeeding but the next input tells it to correct its mistake and thus, the error function increases first as soon as refeeding is instantiated but then converges back. The RMSE on the holdout set decreased to 0.928.

Most of the ideas in this project came from 2 papers: Training Deep AutoEncoders for Collaborative Filtering and AutoRec: Autoencoders Meet Collaborative Filtering. The NVIDIA paper uses SELU instead of ReLU. I tried doing that but error value kept on diverging, so I stopped the training. Maybe training with SELU activation function requires more time. Some papers mention that rather than training the model on each user, it’s better to train the network on each item since the user-item matrix is a tall matrix meaning that there are more ratings available for each product than for each user. This should work and give slightly better results but I don’t see a practical application of this approach as the model size will get huge with so many users as input features and there will be scalability issues in the deployment of the model.
Show me the code
Code: GitHub
One other thing I tried was to use Variation Autoencoder for collaborative filtering but they gave poor performance compared to above-described methods. The latent space of the VAE is not discrete but is assumed to follow a standard normal. This helps in generating a continuous latent space which allows you to explore more variations on your data. The objective function of VAE is to minimize MSE Loss and KL divergence loss simultaneously (scaled by an annealing coefficient). MSE loss acts as the reconstruction loss while generating output from the latent space and the KLD loss makes sure that given an instance, the encoder generates a probability distribution (posterior) which is similar to the prior of the latent space. Thus, VAEs are better as generative models and may not be as good as standard autoencoders for this recommendation system. But I didn’t try out much hyperparameter tuning on the VAE model built, so I won’t and I can’t say much of why they didn’t perform as well.
Thanks,
Ashwin